前言

上一篇介紹到的神經網路流程為
1.輸入
2.權重.偏權重
3.活化函數
4.重複2 ~ 3步驟(依網路深度)
5.輸出函數
6.損失函數
7.計算梯度，數值微分(偏微分)
8.訓練權重(使用梯度下降)
9.重複2 ~ 8步驟(依訓練次數等等)

當網路層數變多或維數變大若計算梯度則所需的計算量會變很大，因此神經網路之父提出了反向傳播，在上次我們說道不符合人類思想，但仔細想想這其實是人類的"反思"，接下來介紹反向傳播是如何求出偏移量的。這裡單純用公式推倒介紹若有興趣可以買書看圖解。
筆記資料來自於:歐萊里深度學習。

正向傳播

在先前介紹的步驟和使用公式計算都是屬於正向，你可以想像每一個步驟計算完在傳給下一個步驟，也就是跟平常一樣由左至右的算法。

例如，函數f(x) = W1 * x + b1。
f(x)對W1的偏微分(變化)，帶入上次提到的數值微分得到x。
f(x)對b1的偏微分(變化)，帶入上次提到的數值微分得到1。

例如，有三層權重(三種函數)。

• 第一層f(x) = W1 * x + b1。
• 第二層g(x) = W2 * x + b2。
• 第三層h(x) = W3 * x + b3。
  這時候我們計算神經網路時的公式會是h(g(f(x)))，一樣使用數值微分，則要計算。
  h(g(f(x)))對W3的偏微分(變化)，h(g(f(x)))對b3的偏微分(變化)。
  h(g(f(x)))對W2的偏微分(變化)，h(g(f(x)))對b2的偏微分(變化)。
  h(g(f(x)))對W1的偏微分(變化)，h(g(f(x)))對b1的偏微分(變化)。

由此可知使用數值微分計算量是很可觀的，接著介紹反向傳播可以解決計算量問題，但還是有缺點。

反向傳播

連鎖率

連鎖率在反向傳播的位置相當重要，首先先看下圖一，當我們要得到x / z可拆開為x / y乘上 y / z，這我想大家都很熟悉，然而如圖二，偏微分也是有連鎖率這特質，現在複習完連鎖率，接著直接介紹反向傳播。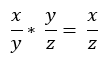

圖一

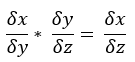
圖二

反向傳播

反向傳播顧名思義就是由最後答案往回推，在這裡拿來推導梯度。
剛才提到的神經網路h(g(f(x)))，如我們最後輸出結果y為1，所以dy = 1(圖一)使用連鎖率結果為：
假設x3 = g (f(x)), x2 = f(x), x = x1。

1.dy * h(x3)對W3的偏微分(變化) = dW3，dy * h(x3)對b3的偏微分(變化) = db3，dy * h(x)對x的偏微分(變化) = dx3。(圖二)

2.dx3 * g(x2)對W2的偏微分(變化) = dW2，dx3 * g(x2)對b2的偏微分(變化) = db2，dW2 * g(x)對x的偏微分(變化) = dx2。(圖三)

3.dx2 * f(x1)對W3的偏微分(變化) = dW1，dy * f(x1)對b1的偏微分(變化) = db1，最後的x不用在計算因為x是輸入，除非還有經過處理。(圖四)

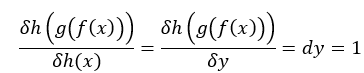
圖一

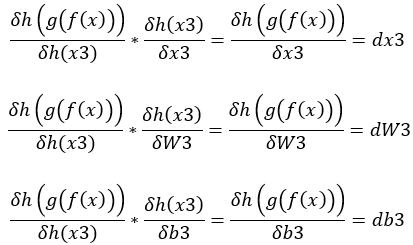
圖二

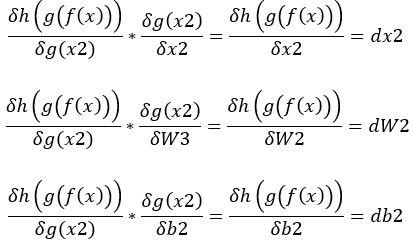
圖三

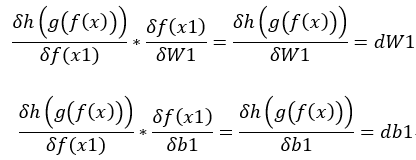
圖四

上述公式足以說明計算量明顯下降很多，但它唯一缺點是，必須由我們先去微分和簡化，接下來介紹權重函數.活化函數.輸出損失函數的反向推導。

乘法的反向傳播

假設f(x, y) = x * y。
一般乘法反向傳播，則dx = y，dy = x，直接人工計算偏微分。

矩陣乘法反向傳播，假設x = ，y = 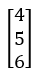，則f(x, y) = [(1 * 4 + 2 * 5 + 3 * 8)] = 32。求dx就是要求每一個x的變化，然而x = [1, 2, 3]對上[4, 5, 8]，此時剛好是W的反轉矩陣，由一般乘法得知dx = y，所以矩陣反向傳播為，。

加法的反向傳播

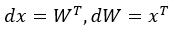假設f(x, b) = x + b。
一般加法反向傳播，假設b = 1，則dx = 1，直接人工計算偏微分。

矩陣加法反向傳播，假設x = 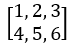，b = 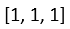(省略寫法，實際上是兩行一樣的)，此時y = 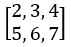。求db變化，由原先加法得知其實就是直接傳給上一層，假如上一層傳來的微分為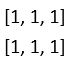，所以db = [2, 2, 2]，這裡我將它解釋為因db原先是2x2但原先將它只寫為1x2所以實際上變化必須把每一層的微分每行做加總，即是b的微分(變化)，dx則不用加總直接傳遞給上一層即可。

權重函數

假設輸入層有兩筆資料向量x = 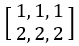，權重為。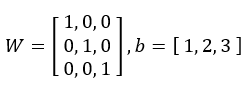
正向傳播：
1.x * W = x1。
2.x1 + b = y。

f(x) = x * W + b =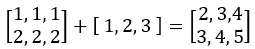
反向傳播，假如上層傳來的為dy，使用正向公式推導回去：
x1 + b = y
1.db = dy每行加總(與d陣列大小相同即可)。
2.dx1 = dy。

x * W = x1
3.dW = 反轉x * dx1。
4.dx = dx1 * 反轉W。
註:第三步和第四步位置要與原先的(x * W)位置相同(矩陣相乘無交換律)

活化函數Sigmoid。

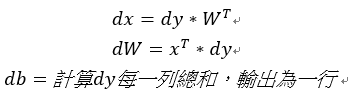
正向傳播：
1.-1 * x = x1
2.e^x1 = x2
3.1 + x2 = x3
4.1 / x3 = y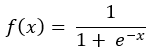

反向傳播，使用正向公式推導回去：
1 / x3 = y
1.dx3 = -1 / x3^2

1 + x2 = x3
2.dx2 = dx3

e^x1 = x2
3.dx1 = dx2 * e^x1

-1 * x = x1
4.dx = dx1 * -1

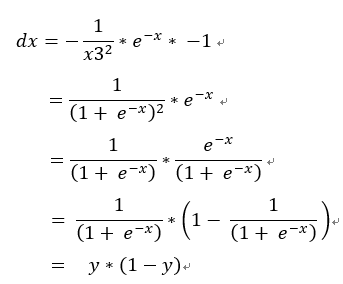
若帶微分除法公式，。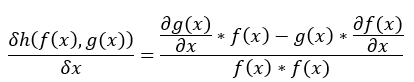

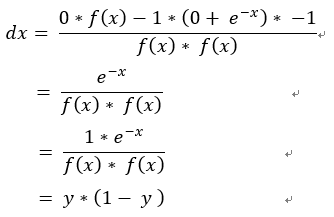
輸出函數+損失函數

正向傳播t為標籤(ont-hot:[0, 0, 1, 0......])：
Softmax:
1.exp(x) = x1
2.sigma(exp(x)) = x2
3.x1 / x2 = x3

Loss Cross:
4.log(x3) = x4
5.x4 * t = x5
6.sigma(x5) = x6
7.x6 * -1 = y

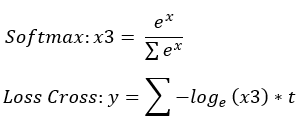
反向傳播，使用正向公式推導回去：
Loss Cross:
x6 * -1 = y
1.dx6 = -1

sigma(x5) = x6
2.dx5 = dx6 = -1(加法直接傳遞)

x4 * t = x5
3.dx4 = dx5 * t = -t

log(x3) = x4
log(x)的微分是1 / x 證明，這裡採用的log都是e為基底，所以不用乘上ln
4.dx3 = dx4 * 1 / x3 = -t / x3

Softmax:
因連鎖率x1 / x2 = x1 * 1 / x2

x1 / x2 = x1 * 1 / x2
5.d(1 / x2) = x1 * dx3 = exp(x) * -t / x3 = -t * sigma(exp(x))
因x1 / x2 = x3，所以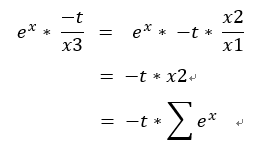

6.dx1 = dx3 * (1 / x2) = -t / exp(x)
因dx3 = -t / x3，所以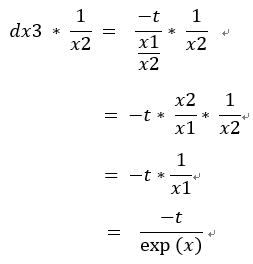

接下來要處理剛剛使用連鎖率的1 / x2求出dx2
1 / x2
7.dx2 = d(1 / x2) * -1 / x2^2 = 1 * sigma(exp(x))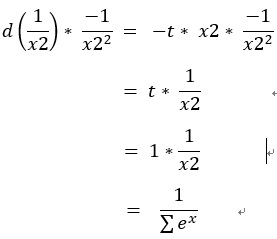

sigma(exp(x)) = x2
8.d(exp(x)) = dx2 (加法直接傳遞)

exp(x)
這裡要注意必須把sigma加總的d(exp(x))和最一開始的dx1做加總，因兩個都是一樣的只是一個拿去加總當分母一個拿去當分子所以最後算出來的變化必須加總。
dx = (d(exp(x)) + dx1) * exp(x) = x3 - t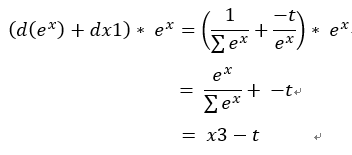

結果x的變化為Softmax輸出 - 標籤資料t 。

結論

最後修改一下原先的神經網路流程，書上所使用forward表示正向backward表示反向。
1.輸入
2.權重.偏權重(forward)
3.活化函數(forward)
4.重複2 ~ 3步驟(依網路深度)
5.輸出 + 損失函數(forward)
7.反向進行backward從輸出+損失開始->重複3 ~ 2(backward)，權重部分記錄dW和db才能更新權重。
8.訓練權重(使用梯度下降)
9.重複2 ~ 8步驟(依訓練次數等等)

＊數值微分用處變為拿來驗證推導的反向傳播是否正確

結語

這次都屬於原理推導，然而後面推廣的技術所用的反向傳播更加不好去計算，我想這就是神經網路所困惑的一個問題吧，最後發現有些地方x1.x2...那邊推導要比較注意，因有的會換回原本公式來做簡化，若有不清楚或錯誤歡迎提問指導。
順便練習了文獻格式，有錯誤麻煩指導。

參考文獻

斎藤康毅、吳嘉芳(譯者)（2017）。Deep Learning：用Python進行深度學習的基礎理論實作。台灣：歐萊禮 。
微分公式。檢自http://webcai.math.fcu.edu.tw/calculus/calculus_html/3-3/law.htm (2018.08.19)